Rückwirkungsabweichung

Wird ein Messgerät in eine Apparatur eingebaut, so verändert sich die ursprüngliche Wirklichkeit. Das Messgerät beeinflusst die physikalische Größe, der die Messung gilt. Seine Rückwirkung auf die Messgröße führt zu einer Messabweichung, die in der für die Messtechnik grundlegenden Norm DIN 1319-1 Rückwirkungsabweichung genannt wird, früher Rückwirkungsfehler.^[1]^[2]

Messung der Temperatur

Zur Messung der Temperatur eines Gases, das durch ein Rohr strömt, wird z.B. ein Widerstandsthermometer eingebaut. Der Messeinsatz und das Thermometerschutzrohr haben eine andere Wärmeableitung als die ursprüngliche Rohrwand. Im Gleichgewicht zwischen dieser erhöhten Wärmeableitung einerseits und der Wärmezufuhr durch das Gas andererseits entsteht im Thermometer eine Temperatur, die von der Gastemperatur abweicht. Die Temperaturdifferenz zur Umgebung wird regelmäßig zu klein bestimmt.

Bei der Vielzahl der Parameter wie Einbautiefe, Durchmesser und Strömungsgeschwindigkeit kann die Abweichung nicht quantitativ angegeben werden. Allenfalls gibt es Erfahrungswerte, wann die Messabweichung vernachlässigbar klein wird.

Messung elektrischer Größen

In elektrischen Schaltungen spricht man auch davon, dass ein Messgerät einen Schaltungseinfluss ausübt, wenn sich durch seine Einfügung die zu messende Größe ändert. Die einfluss- bzw. rückwirkungsfreie Messung des elektrischen Stromes ist nur bei idealer Stromquelle oder der elektrischen Spannung bei idealer Spannungsquelle oder mit idealen Messgeräten möglich. In jedem realen Fall ist mit einer Messabweichung zu rechnen. Ursache ist ein Eigenverbrauch durch seine Mess-Anschlüsse. Wenn hierzu bei elektrischen Messgeräten Kenngrößen bekannt sind, kann man häufig die Rückwirkungsabweichung rechnerisch bestimmen. Als solche Kennzeichen kommen infrage

der Innenwiderstand $R_{i}$
der maximale Spannungs- oder Stromverbrauch:
- beim Strommessgerät der Spannungsabfall $U_{I\mathrm {(MB)} }$ bei Messbereichendwert $I_{\mathrm {MB} }$ ,
- beim Spannungsmessgerät die Stromaufnahme $I_{U\mathrm {(MB)} }$ bei Messbereichendwert $U_{\mathrm {MB} }$ oder der spannungsbezogene Widerstand $\varrho$
gelegentlich (am ehesten bei Messgeräten für Wechselgrößen) die Leistungsaufnahme bei Messbereichendwert.

Im Idealfall ist $U_{I\mathrm {(MB)} }=0$ (kein Spannungsabfall am Strommessgerät mit $R_{i}=0$ ) bzw. $I_{U\mathrm {(MB)} }=0$ (keine Stromaufnahme des Spannungsmessgerätes mit $R_{i}=\infty$ ). Sonst enthält der Messwert stets eine systematische Messabweichung mit negativem Vorzeichen. Wie groß diese ausfällt, ist keine Eigenschaft des Messgerätes alleine, sondern stets das Ergebnis seines Zusammenwirkens mit der Schaltung.

Die Anwendung der Kennzeichen des Eigenverbrauchs soll in Beispielen gezeigt werden. – Die berechnete Abweichung lässt sich nicht dadurch experimentell überprüfen, dass man mit demselben Messgerät die Messung wiederholt.

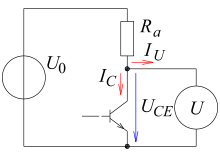
Schaltung mit Spannungsmessgerät

Beispiel 1

In nebenstehender Schaltung sei $U_{0}$ = 24 V; $R_{a}$ = 10 kΩ. Die Ansteuerung des Transistors soll so eingestellt werden, dass $U_{CE}$ = ${\tfrac {1}{2}}U_{0}$ wird. Vom Transistor soll angenommen werden, dass $I_{C}$ unabhängig von $U_{CE}$ ist, eine oberhalb etwa 2 V akzeptable Näherung.
Vom Spannungsmessgerät sind gegeben: $U_{\mathrm {MB} }$ = 15 V und $\varrho$ = 10 kΩ/V. Gefragt ist, wie weit die gemessene und eingestellte Spannung auch diejenige Spannung ist, die sich ergibt, wenn das Messgerät nach der Einstellung entfernt wird.

Bei $U_{\mathrm {MB} }$ = 15 V fließt durch das Messgerät $I_{U\mathrm {(MB)} }=1/\varrho$ = 0,1 mA. Bei einer tatsächlich anliegenden Spannung von 12 V ist der Strom im Verhältnis 12:15 kleiner, also $I_{U}$ = 0,08 mA. Während der Messung fließt durch $R_{a}$ der Strom $I_{C}+I_{U}$ . Nach Entfernung des Messgerätes fließt durch $R_{a}$ nur noch der unveränderte Strom $I_{C}$ , der Spannungsabfall an $R_{a}$ wird um $R_{a}\cdot I_{U}$ = 0,8 V kleiner. Entsprechend steigt $U_{CE}$ auf 12,8 V an. Die absolute Rückwirkungsabweichung beträgt $F$ = – 0,8 V, die relative Abweichung $f$ = − 0,8/12,8 = − 6 %.

Würde die Einstellung mittels eines Messgerätes mit 1 kΩ/V vorgenommen, wäre $I_{U}$ = 0,8 mA und entsprechend die Spannungsänderung an $R_{a}$ durch Entfernung des Messgerätes 8 V. Die Einstellung der Transistoransteuerung kann bei einem solchen Messgerät nach dieser Vorplanung von vorneherein unterbleiben.

Schaltung mit Strommessgerät

Beispiel 2

Die Spannungsquelle sei ideal; der Lastwiderstand sei ohmsch mit $R_{L}$ = 3,0 Ω.

Das Strommessgerät habe die Messbereiche 1 | 3 | 10 | 30 … 1000 mA; Eigenverbrauchskennzeichen $U_{I\mathrm {(MB)} }$ = 0,6 V in allen Bereichen.

Im Messbereich $I_{\mathrm {MB} }$ = 300 mA zeige es gerade Vollausschlag an.

Mit einem Innenwiderstand $R_{i}=U_{I\mathrm {(MB)} }/I_{\mathrm {MB} }$ = 2,0 Ω bestimmt man $U_{0}=I(R_{L}+R_{i})$ = 1,5 V.

Schaltet man den Strommesser um auf den Messbereich 1 A, so wird $R_{i}$ = 0,6 Ω, und der Strom steigt auf 1,5 V/3,6 Ω = 0,42 A an; das ist 40 % mehr als zuerst gemessen. Eine solche Diskrepanz ist ein sicheres Zeichen auf ein defektes Messgerät (was bei dieser Überlegung ausgeschlossen werden kann) oder auf eine Rückwirkungsabweichung. Der Strom nach Entfernung des Strommessers liegt noch höher bei $U_{0}/R_{L}$ = 0,50 A. Der anfangs gemessene Strom weicht gegenüber dem Strom ohne Messgerät ab um −40 %.

Trotz der im 300-mA-Bereich größeren systematischen Messabweichung sollte man nicht auf den 1-A-Bereich umschalten. Denn im 1-A-Bereich sind die aufgrund eines Klassenzeichens zu bedenkenden Fehlergrenzen größer als im 300-mA-Bereich. Die Abweichung durch Rückwirkung ist einfach zu berechnen und korrigierbar; bei Fehlergrenzen wäre der Aufwand zur Korrektur des Messwertes ungleich höher.

Beispiel 3

Die Schaltung und das Messgerät sind dieselben wie zuvor. Nur sind jetzt $U_{0}$ = 70 V und $R_{L}$ = 68 kΩ gegeben, beide mit 1 % relativer Fehlergrenze.

Bei einem erwarteten Strom von etwas mehr als 1 mA wählt man den Messbereich 3 mA aus, zu dem ein Innenwiderstand $R_{i}$ = 0,6 V/3 mA = 0,2 kΩ gehört.

Der angezeigte Strom ist $I_{a}=U_{0}/(R_{L}+R_{i})$ . Der richtige Strom ist $I_{r}=U_{0}/R_{L}$ .

Gemäß der Definition der relativen Messabweichung ist

${\begin{aligned}f&={\frac {I_{a}-I_{r}}{I_{r}}}={\frac {I_{a}}{I_{r}}}-1\\&={\frac {R_{L}}{R_{L}+R_{i}}}-1={\frac {-R_{i}}{R_{L}+R_{i}}}={\frac {-0{,}2}{68{,}2}}=-\;0{,}3\;\%\end{aligned}}$

Nach den Regeln der Fehlerfortpflanzung hat der Strom eine Fehlergrenze von 2 %. Damit ist die Rückwirkungsabweichung des Stromes deutlich geringer als seine Fehlergrenze und kann hier unberücksichtigt bleiben.

Beispiel 4

Der Strom aus einer Batterie mit 1,2 V wird mit einem digitalen Strommesser bei 90 % vom Messbereichendwert gemessen. Wenn bei Messbereichsendwert 0,20 V am Messgerät abfällt, fehlt dem Verbraucher 0,18 V. Das sind 15 % der Batteriespannung; der Verbraucher erhält 85 %. Nach Entfernung des Messgerätes steigt die Spannung am Verbraucher im Verhältnis 100/85 ≈ 1,18, also additiv um 18 %. Bei einer ohmschen Last steigt der Strom in demselben Maße; er fließt um 18 % höher als gemessen.

Einzelnachweise

↑ Paul Profos: Meßfehler: Eine Einführung in die Meßtheorie. Teubner, 1984, S. 63 f
↑ Hans Hart, Werner Lotze, Eugen-Georg Woschni: Meßgenauigkeit. 3. Auflage. Oldenbourg, 1997, S. 22, 49

Basierend auf einem Artikel in:

Wikipedia.de