Aperiodisch

Der Begriff aperiodisch bezeichnet in Physik und Technik – zumindest in der internationalen Normung zur Elektrotechnik – „einen nicht oszillierenden Übergang von einem stationären Zustand in einen anderen“. Dieser Übergang ist ein Ausgleichsvorgang, der zeitlich abklingt.

In der Fachliteratur wird der Begriff „aperiodisch“ uneinheitlich verwendet. Dann hat er die Bedeutung

entweder „nicht periodisch“
oder „ohne oszillierende Anteile“.

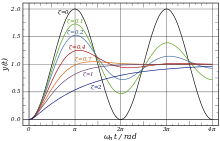
Verschiedene Schwingungsverläufe:
Periodisch ist nur der mit $\zeta =0$ .
Aperiodisch sind bei der gegebenen Definition nur die mit $\zeta \geq 1$ .

Vorgänge

Ein aperiodischer Vorgang ist ein spezieller Verlauf in einem prinzipiell schwingungsfähigen System. Mathematisch wird er als eine der Lösungen der Schwingungsgleichung, einer linearen gewöhnlichen Differentialgleichung, behandelt.

Der Begriff Schwingung wird in der Normung sehr weit gefasst (siehe DIN 1311), der Begriff Periode eher eng.

Periodischer Vorgang

Ein periodischer Vorgang erfüllt die Bedingung

$y(t)=y(t+T)$ für eine beliebige Zeit

und für die Periodendauer $T={\text{konst}}>0$ .

Das bekannteste Beispiel hierfür ist die harmonische Schwingung nach der Gleichung

$y(t)=A\cos(\omega t)$ .

Kriechender Vorgang

Der Verlauf eines sehr stark gedämpften schwingungsfähigen Systems wird als aperiodische Schwingung (Kriechbewegung) zu einer Ruhelage hin bezeichnet. Dafür gilt als eine mögliche Lösung der Schwingungsgleichung

$y(t)=A_{1}\mathrm {e} ^{\lambda _{1}t}+A_{2}\mathrm {e} ^{\lambda _{2}t}$ für $t\geq 0$ und $\lambda _{1},\,\lambda _{2}<0$ .

Dieser Verlauf erfüllt beide oben genannte Bedeutungsmöglichkeiten eines aperiodischen Verlaufs; er ist „nicht periodisch“ und „ohne oszillierende Anteile“.

Die Schwingungs-Differentialgleichung liefert auch die Lösung des aperiodischen Grenzfalls, der sich wie der Kriechfall verhält, aber mathematisch an der Grenze zum Schwingfall liegt.

Schwingender, aber nicht periodischer Vorgang

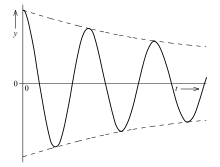
Diese schwach gedämpfte, nicht periodische Schwingung enthält einen oszillierenden Anteil

Dieser befristete Schwingungsimpuls eines PAL-Fernsehsignals enthält einen oszillierenden Anteil

Ferner gibt es nichtperiodische Schwingungen mit einem über eine Ruhelage hinwegschwingenden Verlauf. Dazu gehört die abklingende Schwingung eines schwach gedämpften schwingungsfähigen Systems. Dafür gilt als eine mögliche Lösung der Schwingungsgleichung

$y(t)=A\mathrm {e} ^{-\delta t}\cos(\omega t)$ für $t\geq 0$ und $\delta >0$ .

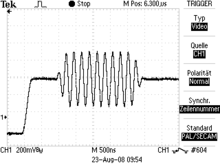
Auch der Sinusschwingungsimpuls (Burst-Signal; in der Tontechnik: Tonimpuls) gehört zu den nichtperiodischen Schwingungen. Er ist nur von kurzer Dauer.

Beide Beispiele erfüllen die Bedeutungsmöglichkeit eines aperiodischen Verlaufs im Sinne von „nicht periodisch“, aber sie erfüllen nicht die Bedeutungsmöglichkeit eines aperiodischen Verlaufs im Sinne von „ohne oszillierende Anteile“. Somit genügen sie auch nicht der genormten Definition.

Weitere Verwendung

Die Verwendung des Begriffs „aperiodisch“ in Physik und Technik über die Elektrotechnik hinaus wird durch einige Beispiele belegt.

In Chr. Gerthsen, H. O. Kneser: Physik: Ein Lehrbuch zum Gebrauch neben Vorlesungen. Springer, 11. Aufl., 1971 (Physik, allgemeine Schwingungslehre) wird eine Bewegung eines Körpers aperiodisch, wenn er allmählich in seine Ruhelage zurückkehrt, ohne über sie hinauszuschwingen.
In E. Truckenbrodt: Fluidmechanik: Band 2: Elementare Strömungsvorgänge … . Springer, 1980 (Strömungstechnik) kann beim langsamen Schließen der Druckrohrleitung einer Wasserkraftanlage eine alternierende, jedoch abklingende Druckschwingung oder eine aperiodisch abklingende Druckschwingung auftreten.
In Eberhard Seiler (Hrsg.): Grundbegriffe des Meß- und Eichwesens. Vieweg, 1983 (Messtechnik) ist ein Messgerät aperiodisch gedämpft, wenn dessen beweglicher Teil die Gleichgewichtslage ohne Schwingungen einnimmt – im Gegensatz zu einem Messgerät mit Schwingungsdämpfung, das die Gleichgewichtslage nach einigen Schwingungen einnimmt.
In Wolfgang Schneider: Praktische Regelungstechnik: Ein Lehr- und Übungsbuch für Nicht-Elektrotechniker. Springer, 1994 (Regelungstechnik) werden je nach Dämpfungsgrad folgende Fälle unterschieden:

$D>1$ aperiodisch kriechend,
aperiodischer Grenzfall,
$0<D<1$ abklingendes Schwingen,
Dauerschwingung,
aufklingendes Schwingen.

Basierend auf einem Artikel in:

Wikipedia.de