Lock-in-Effekt (Physik)

Unter Lock-in-Effekt versteht man die gegenseitige Beeinflussung schwach gekoppelter Oszillatoren.

Erste Beobachtung

Der Lock-in-Effekt wurde wahrscheinlich als erstes von Christiaan Huygens beobachtet. Er berichtet in seinem 1673 erschienenen Buch Horologium Oscillatorium von einem merkwürdigen Phänomen, das er bei Pendeluhren beobachtete.

Auf Schiffen verwendete man zur Navigation kardanisch aufgehängte Pendeluhren. Für den Fall, dass eine Uhr ausfallen sollte, führte man meist zwei gleiche Uhren mit sich. Huygens beobachtete nun, dass zwei Uhren auf einem solchen Schiff nicht nur im Rahmen ihrer Präzision ungefähr gleich gingen, sondern exakt gleich. Sie tickten immer im gleichen Augenblick. Selbst wenn man die Übereinstimmung absichtlich störte, synchronisierten sich die Pendel in kurzer Zeit wieder, in diesem Falle bewegten sich die Pendel im Gegentakt (gegenphasig, spiegelsymmetrisch).

Dieses Phänomen trat auch nur dann auf, wenn die Uhren beide präzise eingestellt waren. Lief eine Uhr deutlich schneller als die andere, kamen sie nicht zur Übereinstimmung.

Huygens' Deutung war, dass über den Balken, an dem beide Uhren hingen, eine Schwingung übertragen wurde. Die Bewegung des Balkens war jedoch so gering, dass sie nicht sichtbar war.

Dieser Effekt wurde auch in Sternwarten an deren hochpräzisen Pendeluhren beobachtet, wenn diese an der gleichen Wand aufgehängt waren. Nach Verdrehung der senkrechten Achse einer Uhr um 90 Grad trat diese Spontansynchronisation nicht mehr auf.

Allgemeine Beschreibung

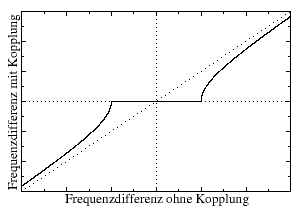
Der Lock-in-Effekt führt bei einer Frequenzdifferenz ungekoppelter Oszillatoren unterhalb der Lock-in-Schwelle dazu, dass bei einer Koppelung beide mit der gleichen Frequenz schwingen. Die Lock-in-Schwelle hängt hierbei von der Stärke der Kopplung ab. Ist die Frequenzdifferenz größer als die Lock-in-Schwelle, führt die Koppelung der Oszillatoren zu einer Reduzierung der Differenzfrequenz.

Dieser Effekt tritt nicht nur bei mechanischen, sondern auch bei allen anderen Schwingungen auf. Auch elektrische Schwingkreise und Laserresonatoren zeigen dieses Phänomen. Insbesondere beim Laserkreisel wird die Genauigkeit im Wesentlichen durch den Lock-in-Effekt beschränkt.

Die Frequenzdifferenz schwach gekoppelter Oszillatoren beträgt

$\Delta f={\sqrt {f_{0}^{2}-f_{L}^{2}}}$

wobei $f_{0}$ für die Frequenzdifferenz ohne Kopplung und f_L für die Lock-in-Schwelle steht.

Literatur

C. Huygens: Die Pendeluhr - Horologium Oscillatorium, Hrsg.: A. Heckscher, A. v. Oettingen, Verlag von Wilhelm Engelmann, Leipzig (1913) S. 24.
R. Rodloff: Gibt es den optischen Superkreisel?, Z. Flugwiss. Weltraumforsch. 18, 2 - 15 Springer-Verlag (1994).

Basierend auf einem Artikel in:

Wikipedia.de