
Satz von Rolle
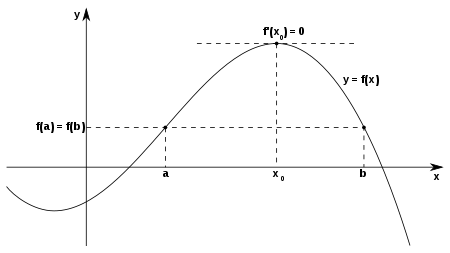
Der Satz von Rolle (benannt nach dem französischen Mathematiker Michel Rolle) ist ein zentraler Satz der Differentialrechnung.
Aussage
Seien
und
eine stetige Funktion, die im
offenen Intervall
differenzierbar
ist. Erfüllt sie
,
so gibt es eine Stelle
mit
.
nterpretation
Anschaulich bedeutet dies: Auf dem Graphen der Funktion
gibt es zwischen zwei Kurvenpunkten mit übereinstimmenden Funktionswerten
mindestens eine Stelle, an der die Steigung gleich null ist. An dieser Stelle
liegt die Tangente waagrecht und damit
parallel zur x-Achse. Der Satz besagt damit insbesondere, dass zwischen zwei
Nullstellen einer differenzierbaren Funktion eine Nullstelle der Ableitung
liegt. Der Satz von Rolle ist ein Spezialfall des Mittelwertsatzes
der Differentialrechnung, dieser lässt sich umgekehrt leicht aus dem Satz
von Rolle beweisen.
Visualisierungen
-
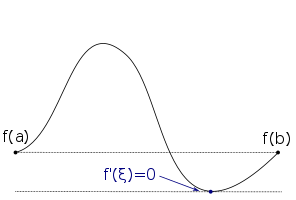 Funktion, die ein Minimum innerhalb des Definitionsbereichs hat. Dort ist die Ableitung gleich null.
Funktion, die ein Minimum innerhalb des Definitionsbereichs hat. Dort ist die Ableitung gleich null. -
 Die Funktion
Die Funktionbesitzt im Inneren des Definitionsbereichs nur ein Maximum und kein Minimum. An dieser Stelle ist die Ableitung null.
-
 Die Funktion
Die Funktionbesitzt im Inneren des Definitionsbereichs nur ein Minimum und kein Maximum. An dieser Stelle ist die Ableitung null.
-
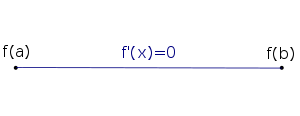 Wenn die Funktion konstant ist, dann ist die Ableitung überall gleich null.
Wenn die Funktion konstant ist, dann ist die Ableitung überall gleich null.
Beweis
Da
über dem kompakten Intervall
stetig ist, nimmt sie (nach dem Satz
von Weierstraß) an einer Stelle
ein Minimum und an einer Stelle
ein Maximum an. Ist
nicht konstant, so muss wegen
mindestens
oder
gelten. Diese Extremalstelle sei mit
bezeichnet. Ist
konstant, so ist
eine Extremalstelle im Inneren des Intervalls
.
Ist die innere Extremalstelle
eine Maximalstelle, so folgt aus der Differenzierbarkeit
von
an der Stelle
,
dass
Somit ist .
Ist
eine Minimalstelle von
,
so ist
eine Maximalstelle von
und wir erhalten
und somit
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.02. 2019