Zissoide des Diokles

Zissoide

Die Zissoide des Diokles (auch: Kissoide des Diokles) ist eine spezielle Kurve 3. Ordnung, die von dem griechischen Mathematiker Diokles (um 200 v. Chr.) beschrieben wurde, um mit diesem Hilfsmittel das Problem der Würfelverdoppelung (auch als delisches Problem bekannt) zu lösen. (Mit Zirkel und Lineal allein ist diese Konstruktionsaufgabe nicht zu schaffen.) Der Name stammt von dem griechischen Wort κισσοειδής (kissoeidēs) für efeuförmig.

Gleichungen der Zissoide

Kartesische Koordinaten: $y^{2}\,(2a-x)-x^{3}=0$
Parametergleichung: $x={\frac {2at^{2}}{1+t^{2}}};\qquad y={\frac {2at^{3}}{1+t^{2}}}$
Polarkoordinaten: $r={\frac {2a}{\cos(\varphi )}}-2a\cos(\varphi )=2a\sin \varphi \tan \varphi$

Eigenschaften der Zissoide

Zissoide als Fußpunktkurve

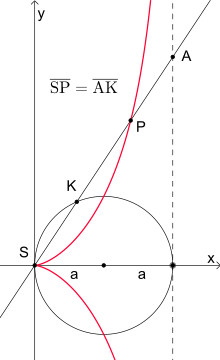
Die Punkte der Zissoide sind gekennzeichnet durch folgende geometrische Eigenschaft: Gegeben seien ein Kreis mit Radius a, ein Punkt S auf diesem Kreis und diejenige Tangente, die diesen Kreis im Punkt gegenüber von S berührt. Bezeichnet man nun für einen beliebigen Punkt P der Zissoide den Schnittpunkt der Geraden SP mit dem Kreis als K und den Schnittpunkt von SP mit der erwähnten Kreistangente als A, so sind die Streckenlängen $\overline {SP}$ und $\overline {KA}$ gleich groß (Diese Eigenschaft folgt direkt aus der Definition allgemeiner Zissoiden).
Die Gerade der Gleichung $x\,=2a$ ist Asymptote der Kurve.
Die Fläche, die von der Zissoide und ihrer Asymptote begrenzt wird, hat den Flächeninhalt $3\,\pi a^{2}$ .
Die Zissoide ergibt sich auch als Fußpunktkurve einer Parabel, wenn man deren Scheitelpunkt als Bezugspunkt wählt.

Literatur

Dörte Haftendorn: Kurven erkunden und verstehen: Mit GeoGebra und anderen Werkzeugen. Springer, 2016, ISBN 9783658147495.

Basierend auf einem Artikel in:

Wikipedia.de