Isokline
Der Begriff Isokline (von griech. ísos = gleich und klínein = neigen) bedeutet in der Mathematik und in der Geophysik eine Kurve gleicher Neigung.
Isoklinen in der Mathematik
In der Mathematik sind Isoklinen ein Hilfsmittel zur graphischen Integration, also zur zeichnerischen Bestimmung von Näherungslösungen einer Differentialgleichung.
Für eine explizite Differentialgleichung
ist jede Kurve mit einer Gleichung des Typs
(bei konstantem
)
eine Isokline. In den Schnittpunkten verschiedener Lösungskurven der
Differentialgleichung mit dieser Isokline haben diese Lösungskurven die gleiche
Steigung
(nämlich
)
und damit den gleichen Neigungswinkel gegenüber der
-Achse.
Beispiel
Für die Differentialgleichung
lautet eine Isoklinengleichung
beziehungsweise
.
Die Isoklinen in diesem Beispiel sind also die Geraden durch den Ursprung mit
Ausnahme der
-Achse.
Die Lösungen der Differentialgleichung haben (zumindest lokal) die Form
.
Die zugehörigen Lösungskurven sind für
Parabeln;
für
erhält man die
-Achse
als weitere Lösungskurve.
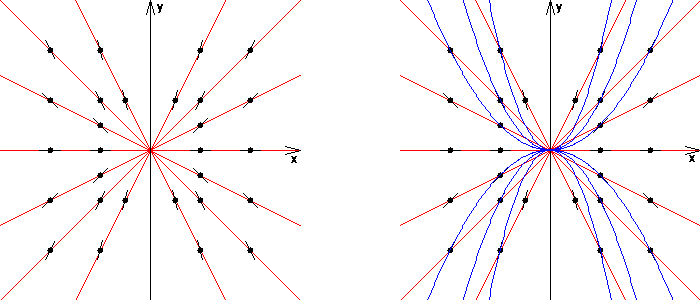
Die beiden Skizzen zeigen einige der Isoklinen (rot). Aus den kurzen Geradenstücken (Linienelementen) lässt sich jeweils die zugehörige Steigung ablesen. In der rechten Skizze sind zusätzlich einige Lösungskurven (blau) eingezeichnet.
Isoklinen in der Geophysik
In der Geophysik wird der Begriff Isokline für Linien gleicher magnetischer Inklination verwendet. Eine solche Isokline verbindet Punkte miteinander, in denen die Feldlinien des Erdmagnetfelds den gleichen Winkel gegenüber der Erdoberfläche einschließen.
Nullkline
Einen Sonderfall stellt die Nullkline
dar, für die gilt .
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.07. 2021