Tragfläche

Die Natur ist das Vorbild

1. Winglet 2. Low Speed Querruder 3. High Speed Querruder 4. Landeklappenträgerverkleidung 5. Krügerklappe 6. Vorflügel 7. innere Flaps 8. äußere Flaps 9. Störklappen 10. Luftbremse 11. Vortex Generator

Die Tragfläche (auch als Flügel, Tragflügel bezeichnet) ist das Bauteil eines Flugkörpers (einschließlich Auftriebshilfen), dessen Hauptaufgabe in der Erzeugung dynamischen Auftriebs bei möglichst geringem Luftwiderstand besteht.

Zu diesem Zweck haben Tragflächen ganz bestimmte Formen, die in Abhängigkeit von Geschwindigkeits- und Höhenbereich, in dem sie verwendet werden, aufgrund der Erkenntnisse der Aerodynamik optimiert sind.
Die Form wird mit Hilfe der Profil- und Tragflügelgeometrie beschrieben.

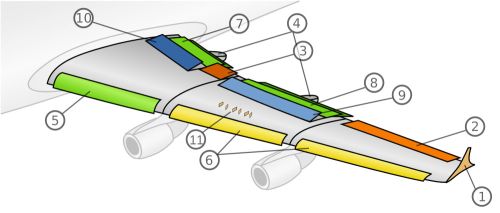
Tragflügelgeometrie

vergl.: Profifgeometrie

Tragflügelgeometrie faßt die charakteristischen geometrischen Merkmale von Tragflügeln zusammen von deren Größe

der Auftriebs- und
der Widerstands- sowie
der Momentenbeiwert

und deren Abhängigkeit von der Anstömgeschweindigkeit eintschieden beeinflußt werden. Außerdem hat die Tragflügelgeometrie einen Starken Einfluß auf das Stabilitätsverhalten des Flugkörpers.
Zu den wichtigsten geometrischen Merkmalen des Tragflügels gehören:

Spannweite b
tragende Fläche
Flügelfläche
laufende Tiefe (von der theoretischen Tiefe t₀ bis zur Endtiefe t_e
Pfeilung Χ (Vorderkantenpfeilung, t/4- und Hinterkantenpfeilung)
Streckung λ = b² / A_TF
Verjüngung η = t₀ / t_e

Die genannten geometrischen Merkmale dienen zum Beschreiben der Tragflächen-Grundform in der horizontalen Symetrieebene des Flugkörpers.
Daneben zählen auch:

die V-Form γ
der Einstellwinkel der Tragfläche φ
die geometrische Schränkung ε = φ_w - φ_e

zu den geometrischen Merkmalen.

Spannweite

Der Abstand zwischen A und B bezeichnet die Spannweite dieses Airbus A320

Entfernung zwischen den äußersten Enden des Tagflügels, parallel zur Querachse des Flugzeuges.

Tragende Fläche

Die für den Auftrieb in Betracht kommende gesamte Fläche. Sie ist die Projektion des Flügelumrisses auf eine Ebene, die senkrecht zur Symmetrieebene des Flugzeugs und parallel zur Sehne des größten Flügelprofils verläuft; Formelzeichen: A_TF oder A_tr.

Flügelfläche

Die Flügelfläche an den Tragflächen eines Flugzeugs ist jene Fläche, die vom Flügelgrundriss umschrieben wird.

die Bruttoflügelfläche: Zu ihr zählen neben der glatten Oberfläche des Flügels die Lande- und andere Klappen, ferner die Ruder (Seiten-, Höhen- und Querruder)
- sowie jener Teil der Tragfläche, der in den Rumpf hineinragt, wenn man sich ihre Vorder- bzw. Hinterkante bis zur Flugzeugachse verlängert denkt.
- Übergänge und Verkleidungen zählen nicht zur Flügelfläche.
die Nettoflügelfläche: Sie entspricht der Bruttofläche, doch abzüglich jener Teile, die in den Rumpf hineinragen.
die Benetzte Oberfläche: Sie ist jener Teil der Tragfläche, der einer Luftströmung ausgesetzt ist.

Streckung

Ist definiert als das Verhältnis des Quadrats der Flügelspannweite zur Flügelfläche oder alternativ auch als Verhältnis der Spannweite zur mittleren Tragflügeltiefe (Seitenverhältnis):

$\Lambda ={\frac {b^{2}}{A}}={\frac {b}{t}}$

mit

: Spannweite
: Flügelfläche
: mittlere Tragflügeltiefe

Eine hohe Streckung der Tragfläche verringert den durch Endwirbel hervorgerufenen induzierten Widerstand. Extrem schlanke Flügel bringen jedoch Probleme bei der mechanischen Stabilität des Flügels und bei der Manövrierbarkeit des Flugzeugs. Winglets haben einen Streckungs-vergrößernden Einfluss und bewirken somit eine Reduzierung des induzierten Widerstands.
Die Streckung eines Tragflügels ist wichtig im Unterschallbereich und bei Flugzeugen, die mit hohem Auftriebsbeiwert betrieben werden. Im Überschall gilt dies nicht mehr, wodurch hier auf eine hohe Streckung verzichtet und die aerodynamische Charakteristik eines Tragflügels fast völlig von der Machzahl entkoppelt werden kann. Ein Beispiel hierfür ist der Delta-Tragflügel.

Pfeilung

Beschreibt den Winkel zwischen Tragflügel und Flugzeugquerachse in der Draufsicht. Sie wird an der Vorderkante (Vorderkantenpfeilung), der Hinterkante (Hinterkantenpfeilung) und bei einem Viertel der Flügeltiefe (t/4-Pfeilung) gemessen.

Profil

→ Hauptartikel: Profil (Strömungslehre)

Als Profil bezeichnet man den Tragflächenquerschnitt in Strömungsrichtung. Die Form des Profils dient einerseits dazu, möglichst viel Auftrieb bei möglichst wenig Strömungswiderstand zu erreichen, und andererseits dazu, einen möglichst großen Anstellwinkel-Bereich ohne Strömungsabriss zu ermöglichen. Je nach Konstruktion (Einsatzzweck, Geschwindigkeitsbereich, Flächenbelastung) werden dazu unterschiedliche Profile verwendet.

Berechnung

Die Bruttofläche des Tragflügels wird durch seine Projektionsfläche in der von Längsachse und Querachse aufgespannten Ebene gebildet. Bei einem Rechteckflügel ist die Fläche gleich dem Produkt aus Spannweite und Profiltiefe :

$A=b\cdot l$

Bei üblicher, über die Querachse nicht konstanter Profiltiefe liefert die Integration über die Spannweite die Flügelfläche:

$A=\int \limits _{-{\frac {b}{2}}}^{+{\frac {b}{2}}}l(y)\,dy$

Wenn die Flügel auf beiden Seiten der Ebene, die von der Flugzeug-Längs- und -Hochachse aufgespannt wird, symmetrisch zueinander sind, lässt sich die Rechnung vereinfachen zu:

$A=2\cdot \int \limits _{0}^{+{\frac {b}{2}}}l(y)\,dy$

Bauformen

Seite zurück
Datum der letzten Änderung : Jena, den: 26.02. 2017