NOR-Gatter

Gatter-Typen
	NOT
AND	NAND
OR	NOR
XOR	XNOR

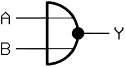
Ein NOR-Gatter (von englisch: not or – nicht oder, oder von englisch nor – noch; auch Peirce-Funktion nach Charles S. Peirce genannt) ist ein Logikgatter mit zwei oder mehr Eingängen A, B, … und einem Ausgang Y, zwischen denen die logische Verknüpfung NICHT ODER besteht. Ein NOR-Gatter gibt am Ausgang genau dann 1 (w) aus, wenn alle Eingänge 0 (f) sind. In allen anderen Fällen, d.h. wenn mindestens ein Eingang 1 ist, wird eine 0 ausgegeben.

Für die NOR-Verknüpfung der Variablen A und B gibt es in der Literatur folgende Schreibweisen:

$A\,\operatorname {NOR}\,B\qquad A\downarrow B\qquad \neg \left(A\lor B\right)\qquad A\overline {\lor }B\qquad \overline {A\lor B}\qquad \overline {A+B}\qquad A\overline {+}B\qquad \neg \left(A+B\right)$

Übersicht

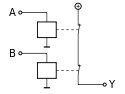
Funktion

Schaltsymbol

Wahrheitstabelle

Relais-Logik

IEC 60617-12

US ANSI 91-1984

DIN 40700 (vor 1976)

$Y = \overline{A \vee B}$

$Y = A \overline{\vee} B$

$Y = \overline{A + B}$

$Y=A\downarrow B$

$Y=A\backslash B$

A	B	Y = A ⊽ B
0	0	1
0	1	0
1	0	0
1	1	0

Realisierung

Die elektronische Realisierung erfolgt zum Beispiel (bei positiver Logik) mit zwei (oder entsprechend mehr) parallel geschalteten Schaltern (Transistoren), die den Ausgang Q auf Masse (logisch 0) legen, sobald einer von ihnen eingeschaltet ist. Sind alle aus, so ist die Masseverbindung unterbrochen und der Ausgang Q liegt auf Pluspotenzial (logisch 1).

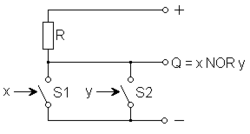Funktionsprinzip eines NOR-Gatters
$Q=x\,\operatorname {NOR}\,y$
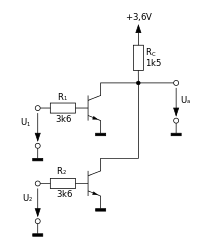Aufbau eines NOR-Gatters in RTL-Technik (Widerstands-Transistor-Logik)
Realisierung eines NOR-Gatters in CMOS-Technologie $a\overline {\lor }b=a\,\operatorname {NOR}\,b$ (ungünstig zu implementieren, da die beiden PMOS-Transistoren seriell geschaltet sind und bei gleicher Chipfläche ohnehin schon hochohmiger als NMOS-Transistoren sind)

Logiksynthese

Gemäß folgender logischer Äquivalenz kann eine NOR-Verknüpfung aber auch allein aus NAND-Gattern aufgebaut werden:

$x\overline {\lor }y=\left[\left(x\overline {\land }x\right)\overline {\land }\left(y\overline {\land }y\right)\right]\overline {\land }\left[\left(x\overline {\land }x\right)\overline {\land }\left(y\overline {\land }y\right)\right]$

Logische Verknüpfungen und deren Umsetzung mittels NOR-Gattern:

Mit der Peirce-Funktion allein sind alle zweiwertigen Wahrheitsfunktionen darstellbar, das heißt jede boolesche Funktion ist äquivalent mit einer Formel, die ausschließlich die NOR-Funktion enthält. Auf Grund dieser Eigenschaft der funktionalen Vollständigkeit nennt man die Peirce-Funktion eine Basis der zweistelligen logischen Funktionen (eine weitere Basis ist die NAND-Funktion).

NOT (Negation, Nicht)	${\overline {x}}$	$\equiv$	$x\overline {\lor }x$

AND (Konjunktion, Und)	$x\land y$	$\equiv$	$\left(x\overline {\lor }x\right)\overline {\lor }\left(y\overline {\lor }y\right)$
NAND (Nicht-Und)	$x\overline {\land }y$	$\equiv$	$\left[\left(x\overline {\lor }x\right)\overline {\lor }\left(y\overline {\lor }y\right)\right]\overline {\lor }\left[\left(x\overline {\lor }x\right)\overline {\lor }\left(y\overline {\lor }y\right)\right]$
OR (Disjunktion, Oder)	$x\lor y$	$\equiv$	$\left(x\overline {\lor }y\right)\overline {\lor }\left(x\overline {\lor }y\right)$
NOR (Nicht-Oder)	$x\overline {\lor }y$	$\equiv$	$x\overline {\lor }y$
XOR (Exklusiv-Oder)	$x\underline {\lor }y$	$\equiv$	$\left(x\overline {\lor }y\right)\overline {\lor }\left[\left(x\overline {\lor }x\right)\overline {\lor }\left(y\overline {\lor }y\right)\right]$
XNOR (Exklusiv-Nicht-Oder)	$x\overline {\underline {\lor }}y$	$\equiv$	$\left[\left(x\overline {\lor }y\right)\overline {\lor }x\right]\overline {\lor }\left[\left(x\overline {\lor }y\right)\overline {\lor }y\right]$

Implikation	$x\rightarrow y$	$\equiv$	$\left[\left(x\overline {\lor }x\right)\overline {\lor }y\right]\overline {\lor }\left[\left(x\overline {\lor }x\right)\overline {\lor }y\right]$
	$x\leftarrow y$	$\equiv$	$\left[x\overline {\lor }\left(y\overline {\lor }y\right)\right]\overline {\lor }\left[x\overline {\lor }\left(y\overline {\lor }y\right)\right]$
Äquivalenz	$x\leftrightarrow y$	$\equiv$	$\left[\left(x\overline {\lor }y\right)\overline {\lor }x\right]\overline {\lor }\left[\left(x\overline {\lor }y\right)\overline {\lor }y\right]$

Verum (immer wahr)	$\top$	$\equiv$	$\left[\left(x\overline {\lor }x\right)\overline {\lor }x\right]\overline {\lor }\left[\left(x\overline {\lor }x\right)\overline {\lor }x\right]$
Falsum (immer falsch)	$\bot$	$\equiv$	$\left(x\overline {\lor }x\right)\overline {\lor }x$

Basierend auf einem Artikel in:

Wikipedia.de